Signed and Unsigned numbers and Binary Data Representation
SIGNED AND UNSIGNED NUMBERS
A binary number may be positive or
negative. Generally, we use the symbol “+” and “−” to represent positive and
negative numbers, respectively. The sign of a binary number has to be
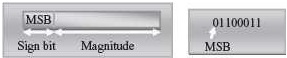
represented using 0 and 1, in the computer. An n-bit signed binary number consists of two parts—sign bit and magnitude. The
left most bit, also called the Most Significant Bit (MSB) is the sign bit. The
remaining n-1 bits denote the magnitude of
the number.
In an n-bit unsigned binary number, the
magnitude of the number n is stored in n bits. An 8–bit unsigned number can
represent data in the range 0 to 255 (28 =
256).
Complement of Binary Numbers
Complements are used in computer
for the simplification of the subtraction operation. For any number in base r,
there exist two complements—(1) r’s complement
and (2) r-1 ’s complement.
Number System
|
Base
|
Complements possible
|
Binary
|
2
|
1’s complement and 2’s complement
|
Octal
|
8
|
7’s complement and 8’s complement
|
Decimal
|
10
|
9’s complement and 10’s complement
|
Hexadecimal
|
16
|
15’s complement and 16’s complement
|
Let us now see how to find the
complement of a binary number. There are two types of complements for the
binary number system—1’s complement and 2’s complement.
·
1’s
Complement of Binary Number is computed by changing the bits 1 to 0 and the bits 0 to 1. For example,
1’s complement of 101 is 010
1’s complement of 1011 is 0100
1’s complement of 1101100 is
0010011
·
2’s
Complement of Binary Number is computed by adding 1 to the 1’s complement of
the binary number. For example,
2’s complement of 101 is 010 +
1 = 011
2’s complement of 1011 is 0100
+ 1 = 0101
2’s complement of 1101100 is
0010011 + 1 = 0010100
The rule to find
the complement of any number N in
base r having n digits is (r − 1)’s
complement—(rn − 1) − N
(r’s) complement2—(rn − 1) − N +
1 = (rn − N)
BINARY DATA REPRESENTATION
A binary number may also have a
binary point, in addition to the sign. The binary point is used for
representing fractions, integers and integer-fraction numbers. Registers are high-speed storage areas
within the Central Processing Unit (CPU) of the computer. All data are brought
into a register before it can be processed. For example, if two numbers are to
be added, both the numbers are brought in registers, added, and the result is
also placed in a register. There are two ways of representing the position of
the binary point in the register—fixed point number representation and floating
point number representation.
The fixed point number representation assumes that the binary point is
fixed at one position either at the extreme left to make the number a fraction,
or at the extreme right to make the number an integer. In both cases, the
binary point is not stored in the register, but the number is treated as a
fraction or integer. For example, if the binary point is assumed to be at
extreme left, the number 1100 is actually treated as 0.1100.
The floatingpoint number representation uses two registers. The first
register stores the number without the binary point. The second register stores
a number that indicates the position of the binary point in the first register.
Fixed Point Number Representation
The integer binary signed number
is represented as follows—
·
For
a positive integer binary number, the sign bit is 0 and the magnitude is a positive binary number.
·
For
a negative integer binary number, the sign bit is 1. The magnitude is
represented in any one of the three ways—
o Signed Magnitude
Representation—The magnitude is the positive binary
number itself.
o
Signed
1 ’s Complement Representation—The magnitude is the 1’s complement
of the positive binary number.
o
Signed
2’s Complement Representation—The magnitude is the 2’s complement
of the positive binary number.
Table 1 shows
the representation of the signed number 18.
 |
| Fixed point representation of the signed number 18 |
Signed magnitude and signed 1’s
complement representation are seldom used in computer
arithmetic.
Let us now perform arithmetic
operations on the signed binary numbers. We use the signed ’s
complement representation to
represent the negative numbers.
·
Addition
of Signed Binary Numbers—The addition of any two signed binary numbers is performed as follows—
o
Represent
the positive number in binary form.(For example, +5 is 0000 0101 and +10 is 0000 1010)
o Represent the negative
number in ’s complement form. (For example, —5 is 1111 1011 and –10 is 1111 0110)
o
Add
the bits of the two signed binary numbers.
o
Ignore
any carry out from the sign bit position.
Please note that the negative
output is automatically in the 2’s complement form.
We get the decimal equivalent of
the negative output number, by finding its 2’s complement, and
attaching a negative sign to the
obtained result.
Let us understand the addition
of two signed binary numbers with the help of some examples.
Example 1: Add +5 and +10.
+5 in binary form, i.e., 0000
0101. +10 in binary form, i.e., 0000 1010.
Example 2: Add −5 and +10.
−5 in ’s complement form is 1111
1011. +10 in binary form is 0000 1010.
Example 3: Add +5 and −10.
+5 in binary form is 0000 0101. −10 in ’s complement
form is 1111 0110. 1111 1011.
The result is in 2’s complement
form. To find its decimal equivalent—
Find the 2’s complement of 1111
1011, i.e., 0000 0100 + 1 = 0000 0101. This is binary
equivalent of + 5. Attaching a
negative sign to the obtained result gives us −5.
Example 4: Add −5 and −10.
−5 in ’s complement form is 1111
1011. −10 in 2’s complement form is 1111 0110.
The result is in 2’s complement
form. To find its decimal equivalent—
Find the ’s complement of 1111
0001, i.e., 0000 1110 + 1 = 0000 1111. This is binary equivalent of +15.
Attaching a negative sign to the obtained result gives us −15.
·
Subtraction of Signed Binary Numbers—The subtraction of signed binary numbers is
changed to the addition of two signed numbers. For this, the sign of the second
number is changed before performing
the addition operation.
(−A) − (+B) = (−A)
+ (−B) (+B in
subtraction is changed to −B in addition)
(+A) − (+B) = (+A) + (−B) (+B in subtraction is changed to
−B in addition) (−A) − (−B) = (−A) + (+B) (−B
in subtraction is changed to +B in addition)
(+A) − (−B) = (+A) + (+B) (−B in subtraction is
changed to +B in addition)
We see that the subtraction of
signed binary numbers is performed using the addition operation.
The hardware logic for the fixed
point number representation is simple, when we use ’s complement for addition
and subtraction of the signed binary numbers. When two large numbers having the
same sign are added, then an overflow may occur, which has to be handled.
The alphabetic data, numeric data,
alphanumeric data, symbols, sound data and video data, are represented as
combination of bits in the computer. The bits are grouped in a fixed size, such
as 8 bits, 6 bits or 4 bits. A code is made by combining bits of definite size.
Binary Coding schemes represent the
data such as alphabets, digits 0−9, and symbols in a standard code. A
combination of bits represents a unique symbol in the data. The standard code
enables any programmer to use the same combination of bits to represent a
symbol in the data.
The binary coding schemes that
are most commonly used are—
·
Extended
Binary Coded Decimal Interchange Code (EBCDIC),
·
American
Standard Code for Information Interchange (ASCII), and
·
Unicode
EBCDIC
·
The
Extended Binary Coded Decimal Interchange Code (EBCDIC) uses 8 bits (4 bits for zone, 4 bits for digit) to represent
a symbol in the data.
·
EBCDIC
allows 28 = 256 combinations of bits.
·
256
unique symbols are represented using EBCDIC code. It represents decimal numbers (0−9), lower case letters (a−z),
uppercase letters (A−Z), Special characters, and Control characters (printable
and non−printable, e.g., for cursor movement, printer vertical spacing, etc.).
·
EBCDIC
codes are mainly used in the mainframe computers.
ASCII
·
The
American Standard Code for Information Interchange (ASCII) is widely used in computers of all types.
·
ASCII
codes are of two types—ASCII−7 and ASCII−8.
·
ASCII-7
is a 7-bit
standard ASCII code. In ASCII-7, the first 3 bits are the zone bits and the
next 4 bits are for the digits. ASCII-7 allows 27 = 128 combinations. 128
unique symbols are represented using ASCII-7. ASCII-7 has been modified by IBM
to ASCII-8.
·
ASCII-8
is an
extended version of ASCII-7. ASCII-8 is an 8-bit code having 4 bits for zone
and 4 bits for the digit. ASCII-8 allows 28 = 256 combinations. ASCII-8 represents 256 unique symbols. ASCII is
used widely to represent data in computers.
·
The
ASCII-8 code represents 256 symbols.
o
Codes
0 to 31 represent control characters (non−printable), because they are used
for actions like, Carriage return (CR), Bell (BEL), etc.
o
Codes
48 to 57 stand for numeric 0−9.
o
Codes
65 to 90 stand for uppercase letters A−Z.
o
Codes
97 to 122 stand for lowercase letters a−z.
o
Codes
128 to 255 are the extended ASCII codes.
Unicode
·
Unicode
is a universal character encoding standard for the representation of text which includes letters, numbers and
symbols in multi−lingual environments. The Unicode Consortium based in
California developed the Unicode standard.
· Unicode
uses 32 bits to represent a symbol in the data.
·
Unicode
allows 232 = 4164895296 (~ 4 billion) combinations.
·
Unicode
can uniquely represent any character or symbol present in any language like
Chinese, Japanese, etc. In addition to the letters; mathematical and scientific
symbols are also represented in
Unicode codes.
·
An
advantage of Unicode is that it is compatible with the ASCII−8 codes. The first 256
codes in Unicode are identical
to the ASCII-8 codes.
·
Unicode
is implemented by different character encodings. UTF-8 is the most commonly
used encoding scheme. UTF stands for Unicode Transformation Format. UTF-8 uses
8 bits to 32 bits per code.
If you wish to see the Unicode
character encoding in MS−Word 2007, do as follows:
<Insert> <Symbol>. A
Symbol dialog box will appear which displays the symbols, and the character
codes in a coding scheme, as shown in Figure 1.
 |
Figure 1: Unicode coding
|






Comments
Post a Comment